Please Execute My Demented Aunt Sally
A revisiting of the dreaded "order of operations."
When math teachers don't know how to teach, you're left not knowing how to math.
Let's change that.
But First...
First, you have to sit through a quick rant about my indignation at the pointless overuse of mnemonic devices to "help" students remember things that
- aren't all that difficult to remember as it is — especially if there's some sort of logical approach underpinning/informing the thing to be memorized, and
- probably won't have any bearing whatsoever on 99.9% of the kids sitting through whatever boring class's vapid subject matter demands memorization of said thing in the first place.
Fun Fact: Instead of just letting me memorize kingdom, phylum, class, order, family, genus, species — a measly seven words, which are hardly a problem for the average human brain to commit to memory — my seventh-grade science teacher also stuck me with the highly-irritating "King Phillip Can't Order Food Greatly Spiced," due to the sheer number of times she regurgitated it at us over the course of that year.
Then, just in passing, she hit us with "Kings Play Chess on Fat Green Stools," while telling us about a positively riveting time when she had encountered that alternative being used by another teacher who apparently preferred it to "King Phillip."
Obligatory Frasier scene:

Then, this same teacher actually gave the class a graded assignment in which we had to go home one night and each come up with our very own seven-word mnemonic... simply for the sake of remembering the principal ranks of modern taxonomy — which, in the grand scheme of things, is actually rather hard to beat in the department of "Underwhelmingly Insignificant Morsel of Knowledge on Which to Baselessly Zero In and Spend the Better Part of Two Full Classes' Worth of Time."
Even in the near-impossible event that every one of us in that class had gone on to major in biology and become taxonomists, this approach still would have proven just about as pointless! But the degradation and the arbitrarity of it also left an immediate and indelible impression on my attitude towards compulsory education... while putting me on higher alert to notice the onslaught of similar situations that would follow throughout the remainder of middle school and high school.
But, yeah... seventh-grade science. Fond memories. Then again, this was the same teacher who assigned me my first and only detention of my entire 12-year public-school stint — for failing to have my mother sign her initials on an exam that I had nearly aced with a 92% score.
While that essay as a whole still pends, suffice it to say that seventh-grade science was absolutely one of the many experiential waypoints on that journey!
Mind blown. What a concept.
So... with that rant having now been ranted, here we go.
Public-Education Math Departments Are Shitty
Middle-school and high-school math teachers, as a whole, seem to consistently fail to recognize that they're teaching an abstractly-dry subject to a classroom full of uncaring teenagers — which is already an uphill battle — and so they go about doing so in just about the most dumb-as-dogshit way I can imagine.
Every generation of students — that is, countless teenagers who will (just in a blanket statistical sense) by and large end up gravitating toward non-mathematical fields anyway — senselessly memorizes the same arbitrary mnemonic device:
Please Excuse My Dear Aunt Sally.
It's never been clear just whose aunt Sally is (is she the teacher's?) — much less why she needs to be excused (did she rip a loud fart at the dinner table?).
But perhaps worst of all is the fact that the mathematical rules this arbitrary sentence is meant to help students remember, come off as being just as arbitrary as the sentence itself — and, as such, students then remember those rules in an uninformed and incorrect capacity.
Thus, the overwhelming majority of students walk away from their childhood math classes with the impression that "PEMDAS" is an arbitrary concoction cooked up by their math teachers just to torment them, rather than being given insight into how and why the order of operations is founded on a basis that is, all things considered, as simplistic and straightforward as it is logical.
Ask anyone over 40 or so (working in a non-math field) to calculate
\[ 6 + 2 * 3 \]
...and chances are overwhelmingly high that they'll just work left to right,
- adding 6 and 2 to get 8,
- then multiplying 8 by 3 to come up with 24,
- and finally balking when they're told that 24 is incorrect.
The fact that this seems to happen at a near societal scale is alarming. But, excepting those precious few who have kept their "math chops" in shape over the decades since high school and college, most people are likely to get the wrong answer on even a simple problem like this one.
What this screams to me is that the logic informing the underlying "rules" of approaching such a problem — even one as simplistic as \(6 + 2 * 3\) — is taught in a way that's neither clear, nor meaningful, nor memorable.
My own recollections indeed corroborate this: I can recall countless teachers insisting, "Ya gotta do the multiplyin' before ya do the addin'!"
...Yet, I can't recall even once when anyone ever explained why.
WHY can't one just compute 6 + 2 * 3 from left to right???
Well, let's find out.
For real.
The Short Answer
The short answer is this:
If you were lucky enough to get any explanation at all for "PEMDAS" when you were a teenager, that's probably the best you would've got.
But the short answer sucks.
It doesn't clarify: It just leads to more whys.
So...
Let's take a more informed look and make it make sense.
The Long Answer
Back to Basics
When you first learned arithmetic as a kid, you probably started with addition, then moved on to subtraction, then got taught multiplication, and finally ended with division.
These were like... the Four Horsemen of basic math, I guess: Four basic operations that all take two numbers (formally called operands), act on those operands in some unique way, and yield a single output:
\[ 2 + 7 = 9 \]
\[ 5 - 3 = 2 \]
\[ 4 * 5 = 20 \]
\[ 12 / 4 = 3 \]
...But what if these operations aren't as different or as unique as they seem?
What if some are sort of just shorthands for others?
Think back, if you can, to your first exposure to multiplication.
It almost certainly began with the rote memorization of "times tables"; but, was there ever a time that you saw something like "4 x 3" and your little-kid brain thought about it as literally
"four times, 3"
...as in...
3 3 3 3
...as in...
3 + 3 + 3 + 3 = 12
— probably someone
Uh... yeah. Sometimes, at least.
It turns out that, when we're dealing with integers — or all rational numbers, really — multiplication is essentially a quicker and more efficient way to write out lots of repeated addition.
But, the perceived benefits and detriments of teaching it that way continue to pose a topic for fierce debate to this day; and so, perhaps none of your teachers ever pointed that relationship out or reinforced it all through school; and so eventually your brain probably stopped thinking of multiplication that way.
Just Add Water
This conscious realization gives us a helpful way to think about multiplication within the order of operations though:
If a multiplication operation is a compaction of successive additions, then it probably just makes sense to you on some intuitive level that we can't simply work with multiplication and addition all willy-nilly, all at once.
We need to learn to think of multiplication as an operation of higher precedence — a cut above addition.
It's like a "just add water" type of deal: You take this dense cuboid of arid multiplicative clay, and you drip a few drops of water on it, and suddenly it expands into some soft, workable addition.
At any rate, this provides a new perspective with which to revisit our
\[ \bold{6 + 2 * 3} \]
We now understand that multiplication is a higher-level operation than addition; so we know we need to take care of that first...
\[ 6 + \textcolor{aqua}{\bold{2 * 3}} \]
\[ 6 + \textcolor{lime}{\bold{6}} \]
\[ \textcolor{lime}{\bold{12}} \]
Turns out the answer really wasn't 24 after all — as a calculator will also confirm for you, if you'd like.
See how the 2 here logically had to serve as a multiplicative operand even though the addition was first in line going from left to right?
THIS is what people forget when they grow up: that the multiplication precedes the addition anyway.
Not simply because "M" comes before "A" in some dumb nonsense expression — like, Pig-Excrement Mnemonics Definitely Always Stink — but rather because you can't very well slice open a bag of multiplication peat moss, dump it into your garden, and expect it to magically mix with the rest of your soft, loamy addition.
That's just dumb.
But, trust me; it's dumb.
You have to add water first. (And, in the case of peat moss, lots of it.)
Opposite Day
Now, you already know that subtraction and division are the inverses of addition and multiplication, respectively:
- subtraction is the opposite of addition
- division is the opposite of multiplication
Starting with subtraction, we can see this in action by examining what happens when we add any arbitrary number with its additive inverse (which is a fancy way of saying "the negation of said number"):
\(5 - 5 = 0\), just like \(5 + -5 = 0\).
Observe how a subtractive operation can be turned into addition, simply by negating the second operand:
\(7 - 3 = 4\), just like \(7 + -3 = 4\).
So, yeah... It sure looks like a minus sign could just as easily be called a "plus-negative" sign.
That's because subtraction is addition in reverse.
This means, then, that addition and subtraction are on the same level of operational precedence.
Thus, when we're approaching a problem that contains both addition and subtraction, we can merely handle them from left to right:
\[ 6 – 3 + 7 + 4 – 9 + 3 – 2 – 2 = \bold{?} \]
Hopefully you came up with an answer of 4. (If you didn't, take a moment to determine why: We're just working from left to right in this case.)
The key takeaways here are twofold:
- Addition and subtraction are equal in precedence (because they're inversions of the same operation), and so you perform them both simultaneously (working from left to right, of course)...
- ...And they are both at the lowest level of precedence — because, unlike other higher-level operations that "unpack" into addition or subtraction (the way we've seen how multiplying is essentially just adding), there is nothing simpler into which addition or subtraction boil down. They are the bottom, and so you perform them last.
Divide and Conquer
Everything we've just established about subtraction with respect to addition is also true of division with respect to multiplication...
Dividing is simply an inversion of multiplying: Instead of successively adding a number numerous times, we're technically just subtracting some number from another number numerous times.
For example, when we say 6 / 2, we essentially want to know how many sets of two can be pulled out of six:
\[ 6 - 2 = 4 \]
\[ 4 - 2 = 2 \]
\[ 2 - 2 = 0 \]
If we count how many times we subtracted, we get our answer: 3
While the additive inverse of a number is that number's negative, the multiplicative inverse (also commonly called its reciprocal) is
\[ \frac{1}{number} \]
So, for example, the reciprocal of 7 is \(\frac{1}{7}\)
If we multiply these together, we just get seven divided by seven, or 1.
Unlike in addition, where the number 0 is called the "additive identity" (because adding zero to any number simply yields that exact same number), the multiplicative identity is the number 1 — because you can multiply (or divide) any number by 1 and you'll get that same exact number.
\[ 9 * 1 = 9 \]
\[ 9 / 1 = 9 \]
\[ 9 * 1/9 = 1 \]
\[ 9 / 9 = 1 \]
Division of Labor
Remember how a minus sign is basically a "plus-negative" sign?
The same is true here, although the wording is a bit less forthcoming:
The point is that division is inverted multiplication, which puts them on the same level of precedence — one level above addition and subtraction. And, when you're dealing with both multiplication and division, you again just work left to right:
\[ 3 / 3 * 6 * 2 / 4 = \bold{?} \]
Hopefully you came up with a 3.
If you didn't, take another look and find out what went wrong: You just have to work left to right here, since it's exclusively multiplication and division, and each takes the same level of precedence as the other.
And of course, the ultimate takeaway is that our two levels of precedence so far are now as follows:
Level 2: Multiplication & Division
Level 1: Addition & Subtraction
Given a math problem that contains any combination of addition, subtraction, multiplication, and division, you simply have to work top to bottom down this list, going from left to right through the problem at each level of operational precedence.
Nope. So then, what's the point?
Putting it All Together
Before we move on into new territory, let's spend a few minutes practicing what we've already learned.
We're going to go through a series of questions now — starting off very basic and working our way into increasing complexity... But ALL of these problems can be done in your head.
Remember, this is still just basic arithmetic! There's nothing scary here: The numbers are small, and it's all about the order of operations.
Question 1
\[ \bold{4 + 8 / 2 = ?} \]
Click for Question 1 answer...
\[ 4 + 8 / 2 = \textcolor{aqua}{\bold{?}} \]
Division takes precedence over addition:
\[ 4 + \textcolor{aqua}{\bold{8 / 2}} = ? \]
\[ 4 + \textcolor{lime}{\bold{4}} = ? \]
Then just perform the addition:
\[ \textcolor{aqua}{\bold{4 + 4 = ?}} \]
\[ \textcolor{lime}{\bold{8}} \]
Question 2
\[ \bold{9 * 2 / 2 - 7 = ?} \]
Click for Question 2 answer...
\[ 9 * 2 / 2 - 7 = \textcolor{aqua}{\bold{?}} \]
Multiplication and division take the same precedence, working from left to right:
\[ \textcolor{aqua}{\bold{9 * 2}} / 2 - 7 = ? \]
\[ \textcolor{lime}{\bold{18}} / 2 - 7 = ? \]
\[ \textcolor{aqua}{\bold{18 / 2}} - 7 = ? \]
\[ \textcolor{lime}{\bold{9}} - 7 = ? \]
Then perform the subtraction:
\[ \textcolor{aqua}{\bold{9 - 7}} = ? \]
\[ \textcolor{lime}{\bold{2}} \]
Question 3
\[ \bold{12 - 6 / 3 + 4 = ?} \]
Click for Question 3 answer...
\[ 12 - 6 / 3 + 4 = \textcolor{aqua}{\bold{?}} \]
Perform the division first:
\[ 12 - \textcolor{aqua}{\bold{6 / 3}} + 4 = ? \]
\[ 12 - \textcolor{lime}{\bold{2}} + 4 = ? \]
Addition and subtraction take the same precedence, working from left to right:
\[ \textcolor{aqua}{\bold{12 - 2}} + 4 = ? \]
\[ \textcolor{lime}{\bold{10}} + 4 = ? \]
\[ \textcolor{aqua}{\bold{10 + 4}} = ? \]
\[ \textcolor{lime}{\bold{14}} \]
Question 4
\[ \bold{8 - 6 - 1 + 2 * 3 = ?} \]
Click for Question 4 answer...
\[ 8 - 6 - 1 + 2 * 3 = \textcolor{aqua}{\bold{?}} \]
Multiplication precedes addition and subtraction:
\[ 8 - 6 - 1 + \textcolor{aqua}{\bold{2 * 3}} = ? \]
\[ 8 - 6 - 1 + \textcolor{lime}{\bold{6}} = ? \]
Then just perform addition and subtraction from left to right:
\[ \textcolor{aqua}{\bold{8 - 6}} - 1 + 6 = ? \]
\[ \textcolor{lime}{\bold{2}} - 1 + 6 = ? \]
\[ \textcolor{aqua}{\bold{2 - 1}} + 6 = ? \]
\[ \textcolor{lime}{\bold{1}} + 6 = ? \]
\[ \textcolor{aqua}{\bold{1 + 6}} = ? \]
\[ \textcolor{lime}{\bold{7}} \]
Question 5
\[ \bold{10 * 2 - 8 + 7 / 7 - 1 * 3 + 4 - 9 = ?} \]
Click for Question 5 answer...
\[ 10 * 2 - 8 + 7 / 7 - 1 * 3 + 4 - 9 = \textcolor{aqua}{\bold{?}} \]
Multiplication and division take precedence, from left to right:
\[ \textcolor{aqua}{\bold{10 * 2}} - 8 + 7 / 7 - 1 * 3 + 4 - 9 = ? \]
\[ \textcolor{lime}{\bold{20}} - 8 + 7 / 7 - 1 * 3 + 4 - 9 = ? \]
\[ 20 - 8 + \textcolor{aqua}{\bold{7 / 7}} - 1 * 3 + 4 - 9 = ? \]
\[ 20 - 8 + \textcolor{lime}{\bold{1}} - 1 * 3 + 4 - 9 = ? \]
\[ 20 - 8 + 1 - \textcolor{aqua}{\bold{1 * 3}} + 4 - 9 = ? \]
\[ 20 - 8 + 1 - \textcolor{lime}{\bold{3}} + 4 - 9 = ? \]
Then perform addition and subtraction, left to right:
\[ \textcolor{aqua}{\bold{20 - 8}} + 1 - 3 + 4 - 9 = ? \]
\[ \textcolor{lime}{\bold{12}} + 1 - 3 + 4 - 9 = ? \]
\[ \textcolor{aqua}{\bold{12 + 1}} - 3 + 4 - 9 = ? \]
\[ \textcolor{lime}{\bold{13}} - 3 + 4 - 9 = ? \]
\[ \textcolor{aqua}{\bold{13 - 3}} + 4 - 9 = ? \]
\[ \textcolor{lime}{\bold{10}} + 4 - 9 = ? \]
\[ \textcolor{aqua}{\bold{10 + 4}} - 9 = ? \]
\[ \textcolor{lime}{\bold{14}} - 9 = ? \]
\[ \textcolor{aqua}{\bold{14 - 9}} = ? \]
\[ \textcolor{lime}{\bold{5}} \]
So...
How did you do?
Hopefully stellar.
But, eww. I don't like the way stellarly looks at all.
Anyway, if you did get tripped up anywhere, consult the work included in the solutions to see where you're getting stuck and how to remedy that.
A Higher Power
Now let's take a look at exponents.
You likely understand these at a rudimentary level already:
\[ 4^{2} = 16 \]
\[ 2^{3} = 8 \]
\[ 3^{4} = 81 \]
But, do you recall what's actually going on "under the hood" of an exponentiated expression?
Sure, we say that four squared is 16. But why?
Well, that's easy: It's because \(4 * 4 = 16\).
Sooo.......... exponents are simply multiplication, which is just addition — though, if multiplication is a "just add water" version of addition, then exponentiation is like a... "just add fire" version.
At any rate, yes, exponentiation is just another higher-precedence shorthand — both for multiplication, and eventually for addition:
\[ 3^{4} = 81 \]
\[ 3 * 3 * 3 * 3 = 81 \]
\[3 + 3 + 3 + 3 + 3 + 3 + 3 + 3 + 3 + 3 + 3 + 3 + 3 + 3 + 3 + 3 + 3 + 3 + 3 + 3 + 3 + 3 + 3 + 3 + 3 + 3 + 3 = 81 \]
As you may have already guessed, this higher precedence simply means that we must deal with exponents in our expressions before we perform any of the four basic arithmetic operations (+ – * /).
Level Up, Buckle Down
For the record, the same holds true for the inverse operations of exponentiation as well: roots and logarithms.
These are more advanced, and so I won't get into them in depth here while we're just trying to refamiliarize ourselves with the order of operations.
But, in a nutshell, those operations work like this:
A root of a number is some other number that yields that number when raised to a certain power:
42 is 16; so we call 4 the "square root of 16" (which we can also write as \(\sqrt{16} = 4\)).
A logarithm, on the other hand, finds the power (or exponent) instead of the root (or base):
We know that 23 = 8; but if we didn't (say, because we're working with far larger numbers than we'd bother memorizing), we could write the reverse as
\[ \log_{2}(8) = ? \]
In plain English, this translates to, "to what power would we need to raise 2 to get 8?"
The Natural Order of Things
Just remember this "natural order" of things, now that you've learned that it comes from a place of logic and not just from some hare-brained math teacher insisting, "...because I said so!"
Level 3: Exponentiation, Roots, & Logarithms
Level 2: Multiplication & Division
Level 1: Addition & Subtraction
So...
\[ 6 + 5 * 3^{2} = ? \]
(You should get 51. Take the time to ensure that you understand why.)
(Psssst!)
Of course, there are always exceptions to every rule... but luckily, in this case the exception is pretty straightforward:
There will be times when you want to override this natural order and ensure that anyone else performing the computation in question will arrive at the answer you intend for them to reach.
In such cases, you have parentheses and brackets at your disposal. These are used to give certain groupings of numbers and operations precedence within an expression.
The best way to show when and why you might want to do this is with a real-world example; so let's look at one...
So, here's some "garden-variety" math for you:
Let's say that big, bad, capitalist Uncle Winter (<—— that's me) tells @Stinks that he'll pay her two pennies for every red tomato she picks and two pennies for every weed she pulls out.
Stinks comes back with 8 tomatoes and says she pulled 3 weeds; so, we have the info we need in order to pay her: We just add the tomatoes and the weeds, and multiply that number by 2 to see how many pennies are owed.
\[ 8 + 3 * 2 \]
Ah, but wait!
The order of operations tells us that we need to multiply 3 * 2 first.
But, in this case, that will give us a "wrong" answer of 14 pennies, when Stinks knows that she is owed 22!
Fear not! Parentheses to the rescue...
\[ (8 + 3) * 2 \]
Now anyone doing payroll will see that, in this particular case, they're meant to add first, and then multiply.
Tax Brackets
You may, on occasion, see brackets in the wild as well:
\[ [7 * (3 - 2)] + 5^{2} / 5 \]
Brackets are basically just parentheses' big brother. You handle them before you do anything else.
Nested parentheses are more common in this case—and you always handle the innermost parentheses first.
Now, before we continue, let's take a crack at that problem above. It's a cut above the others we've done, but just remember the proper order:
- Brackets
- Parentheses
- Exponentiation (and its inverses)
- Multiplication AND Division
- Addition AND Subtraction
Try it yourself, and then consult the solution below if you need to:
Solution...
\[ [7 * (3 - 2)] + 5^{2} / 5 = \textcolor{aqua}{\bold{?}} \]
Brackets come first!
\[ \textcolor{aqua}{\bold{[7 * (3 - 2)]}} + 5^{2} / 5 = ? \]
We start by handling those parentheses:
\[ \textcolor{blue}{[7 * \textcolor{aqua}{\bold{(3 - 2)}}]} + 5^{2} / 5 = ? \]
\[ \textcolor{aqua}{[7 * \textcolor{lime}{\bold{1}}]} + 5^{2} / 5 = ? \]
Now we can tackle the rest of the bracketed portion:
\[ \textcolor{aqua}{\bold{[7 * 1]}} + 5^{2} / 5 = ? \]
\[ \textcolor{lime}{\bold{7}} + 5^{2} / 5 = ? \]
Next up, we have exponentiation:
\[ 7 + \textcolor{aqua}{\bold{5^{2}}} / 5 = ? \]
\[ 7 + \textcolor{lime}{\bold{25}} / 5 = ? \]
Then division:
\[ 7 + \textcolor{aqua}{\bold{25 / 5}} = ? \]
\[ 7 + \textcolor{lime}{\bold{5}} = ? \]
And finally, addition:
\[ \textcolor{aqua}{\bold{7 + 5}} = ? \]
\[ \textcolor{lime}{\bold{12}} \]
Respect the Hierarchy
And that basically concludes how "order of operations" should have been taught when you were a wee tyke.
It's not at all a linear, one-by-one checklist where you go down the line, the way "PEMDAS" implies:
Do all the multiplication, then do all the division. Then do all the addition, and then all the subtraction.
Nope. Wrong.
Rather, it's a hierarchy where operations of varying precedences are ordered accordingly, and you approach them as such...
So, it's more like Maslow's hierarchy of needs...
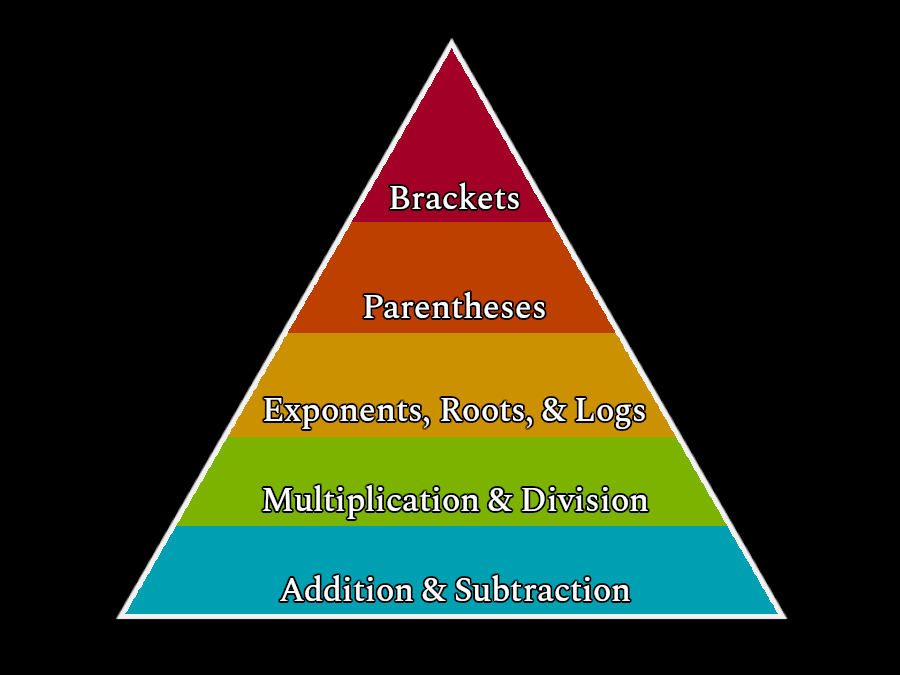
So, I guess it's not like Maslow's hierarchy at all, save for them both being shaped like a triangle.
Do you know how long I spent coloring in that triangle just now though? Like five minutes! So I don't really feel like changing it at this point. <shrug>
But hopefully you get the point: The logic underpinning our order of operations doesn't come from some stupid mnemonic device... and that device we were all taught as kids was never even really all that helpful!
So —
Brother, Please... Excoriate Really Loudly... Mentorly Dipshits... Advocating Stupidity.
— and I hope you got something useful out of this introductory lesson.
It might not feel like we covered a ton; but everything in algebra and beyond builds on these rules, and hence requires understanding of them.
Happy math-ing :)